Tweet
Share
Pin1
Share
1 Shares

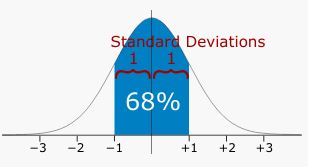
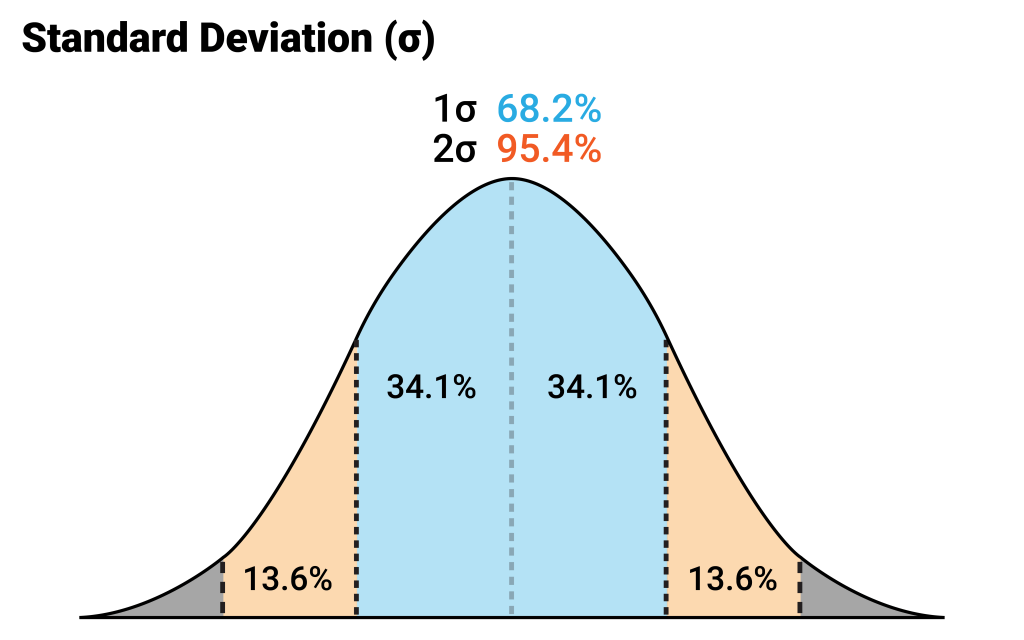
There would be no statistician to calculate standard deviation by hand. The calculations are a bit complicated. Although the risk of making mistakes is high as usual, therefore, a professional statistician will rely on calculating these equations on sheets or computer software programs.

Interesting? In this article, we will show you how we can calculate standard Deviation and variance once for all. The tricky part is figuring these equations ourselves by our hand gives us satisfaction, and on the other part, there would be no happiness calculating the same in any excel sheet or computer program.

Standard Deviation and How to Calculate It?

standard-deviation-calculation

Standard Deviation is the most vital formula to calculate dispersion measurement. It is not like that you need to have the values of mean, mode, and median to get S.D of it. 

Standard Deviation can found by mean itself. However, there are three types of series and which are individual series, discrete series, and frequency distribution series. Let’s have a look!

Three series to calculate:

  1. Individual series
  2. Discrete series
  3. Frequency distribution series

#1 Individual Series:

Usually, we calculate the value of the mean only. But, now we will calculate the deviation of each observation by using this simple formula D= X – Mean. We have to divide the observations square by the deviation and the method for the same given below.

Standard Deviation (σ)= √[∑D²/N]

Here, D= Deviation of an item relative to mean

N= The number of observations

#2 Discrete Series:

In Discrete series, each of the formulae needs frequency. So, the method to calculate Standard Deviation changes accordingly to include frequency in between.

Formula to calculate standard deviation by discrete series is: 

Standard deviation(σ)= √(∑fD²)/N)

Here, D= Deviation of an item relative to the mean calculated as, D= X – Mean.

f= Frequencies corresponding to the observations

N= The Summation of frequency

#3 Frequency distribution series:

The method is the same as the discrete series to calculate the Standard Deviation. The only difference in the frequency distribution series is mid-value of the class is derived, and that can be solved, dividing the upper value, and a lower value and same can use for calculation. Here’s how:

Standard deviation(σ)= √(∑fD²)/N)

Here, D= Deviation of an item relative to the mean calculated as, D= Xi – Mean

f= Frequencies corresponding to the observations

N= The summation of frequency

Variance:

Since we know standard deviation is essential for calculating the dispersion but it arrives from variance itself. However, it is better than the mean deviation because it uses the square of deviation to calculate. Although Variance is using squares, that means it uses mean in the series.

Keeping that in mind, statisticians can use square root for a variance, which is known as standard deviation itself. The formula of calculating Variance is: 

Variance= ( Standard deviation)²= σ×σ

Conclusion: 

Sometimes, it could be challenging to understand the exact equations in standard deviations and variance. The same we need to add in this article that how one can calculate standard deviation and variance to measure the dispersion.